https://www.acmicpc.net/problem/15685
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10) 입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다. 방향은 0, 1, 2,
www.acmicpc.net
문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
-
시작 점
-
시작 방향
-
세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.

즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
-
0: x좌표가 증가하는 방향 (→)
-
1: y좌표가 감소하는 방향 (↑)
-
2: x좌표가 감소하는 방향 (←)
-
3: y좌표가 증가하는 방향 (↓)

출력
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
예제 입력 1
3
3 3 0 1
4 2 1 3
4 2 2 1
예제 출력 1
4
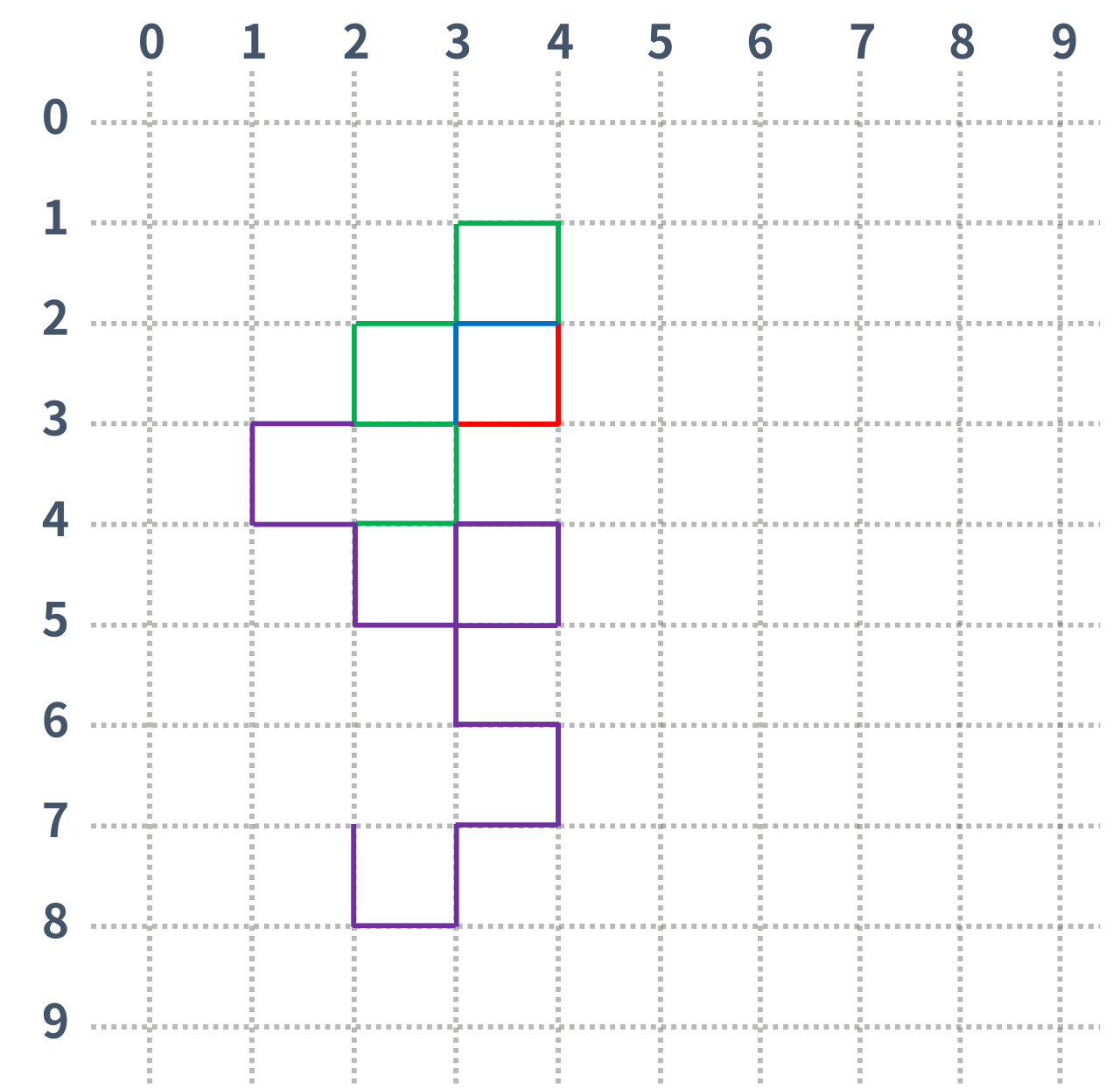
예제 입력 2
4
3 3 0 1
4 2 1 3
4 2 2 1
2 7 3 4
예제 출력 2
11
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
struct dragon{
int x,y,d,g;
};
int map[110][110]={0,};
int N;
dragon d1[21];
int dx[]={1,0,-1,0};
int dy[]={0,-1,0,1};
vector <int> moving;
int count(){
int cnt=0;
for(int i=0;i<105;i++){
for(int j=0;j<105;j++){
if(map[i][j]==1&&map[i+1][j]==1&&map[i+1][j+1]==1&&map[i][j+1]==1){
cnt++;
}
}
}
return cnt;
}
void goDragon(int n){
int ny = d1[n].y;
int nx = d1[n].x;
int nd = d1[n].d;
int ng = d1[n].g;
moving.clear();
map[ny][nx]=1;
moving.push_back(nd);
while(ng--){
int now_size=moving.size()-1;
for(int i=now_size;i>=0;i--){
int temp = moving[i];
temp = (temp+1)%4;
moving.push_back(temp);
}
}
for(int i=0;i<moving.size();i++){
ny = ny + dy[moving[i]];
nx = nx + dx[moving[i]];
map[ny][nx]=1;
}
}
int main(){
// freopen("input.txt","r",stdin);
cin>>N;
for(int i=0;i<N;i++){
cin>> d1[i].x >> d1[i].y >> d1[i].d >> d1[i].g;
}
for(int i=0;i<N;i++){
goDragon(i);
}
int result2 = count();
cout<<result2;
return 0;
}'개발자 > algorithm' 카테고리의 다른 글
| 백준 17779번 : 게리맨더링2 (c++) (0) | 2020.04.17 |
|---|---|
| 백준 14891번 : 톱니바퀴 (c++) (0) | 2020.04.17 |
| 백준 14890번 : 경사로 (c++) (0) | 2020.04.15 |
| 백준 17144번 : 미세먼지 안녕! (c++) (0) | 2020.04.15 |
| 백준 14503번 : 로봇 청소기 (c++) (0) | 2020.04.14 |